secje

(define (square x) (* x x))
(define (smallest-divisor n)
  (find-divisor n 2))
(define (find-divisor n test-divisor)
  (cond ((> (square test-divisor) n) n)
        ((divides? test-divisor n) test-divisor)
        (else (find-divisor n (+ test-divisor 1)))))
(define (divides? a b)
  (= (remainder b a) 0))
(define (prime? n)
  (= n (smallest-divisor n)))
(define (find-prime n k)
  (cond ((even? n) (find-prime (+ n 1) k))
        ((= k 0) #t)
        ((prime? n) (find-prime (+ n 2) (- k 1)))
        ((not (prime? n)) (find-prime (+ n 2) k))))
(define (start-prime-test n start-time k)
  (if (find-prime n k)
      (- (runtime) start-time)))
(define (time-prime-test n k)
  (start-prime-test n (runtime) k))

(time-prime-test 100000000000 3)
;Value: 5.178

(time-prime-test 1000000000000 3)
;Value: 14.943000000000001

(time-prime-test 10000000000000 3)
;Value: 70.16499999999999

(time-prime-test 10000000000 3)
;Value: 1.9200000000000017

总体来说还是比较贴近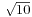

为了能在PLT下面运行

语言包改成了Swindle，调用了primitive called current-milliseconds

(define (runtime) (current-milliseconds))
(define (square x) (* x x))
(define (smallest-divisor n)
  (find-divisor n 2))
(define (find-divisor n test-divisor)
  (cond ((> (square test-divisor) n) n)
        ((divides? test-divisor n) test-divisor)
        (else (find-divisor n (+ test-divisor 1)))))
(define (divides? a b)
  (= (remainder b a) 0))
(define (prime? n)
  (= n (smallest-divisor n)))
(define (find-prime n k)
  (cond ((even? n) (find-prime (+ n 1) k))
        ((= k 0) #t)
        ((prime? n) (find-prime (+ n 2) (- k 1)))
        ((not (prime? n)) (find-prime (+ n 2) k))))
(define (start-prime-test n start-time k)
  (if (find-prime n k)
      (- (runtime) start-time)))
(define (time-prime-test n k)
  (start-prime-test n (runtime) k))

> (time-prime-test 1000 3)
1
> (time-prime-test 10000 3)
1
> (time-prime-test 100000 3)
3
> (time-prime-test 10000000000 3)
1411
> (time-prime-test 100000000000 3)
3727
> (time-prime-test 1000000000000 3)
11193

1.2.1

199
1999
7

Considering an algorithm to be inadequate for the first reason but not for the second illustrates the difference between mathematics and engineering. ——Hal Abelson and Gerald J. Sussman (1996). Structure and Interpretation of Computer Programs. MIT Press, section 1.2.

对一个算法，对第一个原因来讲不合适，但是第二个原因就足够了，这表明了数学和工程的区别。

这个问题有幸得到了裘老师的解答，在此非常感谢，翻译问题感谢小帆同学

指评价一个"算法"是否合适可用。数学讲完全，

绝不能错，错一点
也不行。工程讲可靠，很可靠，出问题的概率极小就可以接受（如，没有一个房子
在任何情况下都不会倒。只要倒的可能性很小就可以）。大致就是这个意思。

(define (square x) (* x x))
(define (fast-prime? n)
  (define (expmod base exp m)
    (cond ((= exp 0) 1)
          ((even? exp)
           (remainder (square (expmod base (/ exp 2) m))
                      m))
          (else
           (remainder (* (remainder base m) (expmod base (- exp 1) m))
                    m))))
  (define (fermat-test a)
    (= (expmod a n n) a))
  (define (test a)
    (cond ((= a n) #t)
          ((fermat-test a) (fermat-test (+ a 1)))
          (else #f)))
  (cond ((= n 1) #f)
        ((= n 2) #t)
        (else (test 1))))

为了在PLT下玩，自己改了下，代码量不够的劣势就显示出来了，如此简单的东东，我做了半天= =

 看了网上的答案，自己改了下

(define (square x) (* x x))
(define (fast-prime? n)
  (define (expmod base exp m)
    (cond ((= exp 0) 1)
          ((even? exp)
           (remainder (square (expmod base (/ exp 2) m))
                      m))
          (else
           (remainder (* (remainder base m) (expmod base (- exp 1) m))
                    m))))
  (define (fermat-test a)
    (= (expmod a n n) a))
  (define (test a)
    (cond ((= a 0) #t)
          ((fermat-test a) (fermat-test (- a 1)))
          (else #f)))
  (test (- n 1)))

(define (square x) (* x x))
(define (fast-prime? n times)
  (define (expmod base exp m)
    (cond ((= exp 0) 1)
          ((even? exp)
           (remainder (square (expmod base (/ exp 2) m))
                      m))
          (else
           (remainder (* (remainder base m) (expmod base (- exp 1) m))
                    m))))
  (define (fermat-test n)
    (define (try-it a)
      (= (expmod a n n) a))
    (try-it (+ 1 (random (- n 1)))))
  (cond ((= times 0) true)
        ((fermat-test n) (fast-prime? n (- times 1)))
        (else false)))

PLT不认random，改用MIT Scheme了，看来要加快emacs的脚步了，越到后面谁知道还会发生什么，现在就是蛋疼的用PLT当编辑器和调试器，edwin做解释器

(define (square x) (* x x))
(define (expmod base exp m)
  (cond ((= exp 0) 1)
        ((even? exp)
         (remainder (square (expmod base (/ exp 2) m))
                    m))
        (else
         (remainder (* base (expmod base (- exp 1) m))
                    m))))

本来x*y%m=b*d%m=((x%m)*(y%m))%m

(define (square x) (* x x))
(define (expmod base exp m)
  (cond ((= exp 0) 1)
        ((even? exp)
         (remainder (square (expmod base (/ exp 2) m))
                    m))
        (else
         (remainder (* (remainder base m) (expmod base (- exp 1) m))
                    m))))

这里设

x

y=a*m+b

x*y%m=(a*m*x+b*x)%m=b*x%m=(x*(y%m))%m得证

x*y%m=((x%m)*(y%m))%m

to see this

we assume that     

x=am+b

y=cm+d

x*y=a*c*m²+a*d*m+b*c*m+b*d

等式两边同时对m取余

x*y%m=(a*c*m²+a*d*m+b*c*m+b*d)%m

我们这样看

(a*c*m²)%m==0

(a*d*m)%m==0

(b*c*m)%m==0

assume

s=k1*m

t=k2*m

p=k3*m

q=k4*m+z

we know that z<m

so     s+t+p+q=(k1+k2+k3+k4)*m+z

therefore       (s+t+p+q)%m==z

所以

(a*c*m²+a*d*m+b*c*m+b*d)%m=b*d%m

即x*y%m=b*d%m=((x%m)*(y%m))%m得证

(gcd 206 40)
(if (= 40 0)
    206
    (gcd 40 (remainder 206 40)))
(if (= (remainder 206 40) 0)      ;1
    40
    (gcd (remainder 206 40) (remainder 40
                                       (remainder 206 40))))
(if (= (remainder 40
                  (remainder 206 40)) 0)   ;2
    (remainder 206 40)
    (gcd (remainder 40
                    (remainder 206 40))
         (remainder (remainder 206 40)
                    (remainder 40
                               (remainder 206 40)))))
(if (= (remainder (remainder 206 40)
                  (remainder 40
                             (remainder 206 40))) 0)    ;4
    (remainder 40
               (remainder 206 40))
    (gcd (remainder (remainder 206 40)
                    (remainder 40
                               (remainder 206 40)))
         (remainder (remainder 40
                               (remainder 206 40))
                    (remainder (remainder 206 40)
                               (remainder 40
                                         (remainder 206 40))))))
(if (= (remainder (remainder 40
                            (remainder 206 40))
                  (remainder (remainder 206 40)
                             (remainder 40
                                        (remainder 206 40)))) 0) ;7 and indeed equal to 0, so continue the next (1)
    (remainder (remainder 206 40)
               (remainder 40
                         (remainder 206 40)))   ;(1)  4
    (gcd (remainder (remainder 40
                               (remainder 206 40))
                    (remainder (remainder 206 40)
                               (remainder 40
                                          (remainder 206 40))))
         (remainder (remainder (remainder 206 40)
                               (remainder 40
                                          (remainder 206 40)))
                    (remainder (remainder 40
                                          (remainder 206 40))
                               (remainder (remainder 206 40)
                                          (remainder 40
                                                     (remainder 206 40)))))))     ;so the result is 1+2+4+7+4=18

(define (fib n)
  (define (fib-iter a b p q count)
    (cond ((= count 0) b)
          ((even? count) (fib-iter a
                                   b
                                   (+ (* p p)
                                      (* q q))
                                   (+ (* q q)
                                      (* 2 p q))
                                   (/ count 2)))
          (else (fib-iter (+ (* b q) (* a q) (* a p))
                          (+ (* b p) (* a q))
                          p
                          q
                          (- count 1)))))
  (fib-iter 1 0 0 1 n))